ABC256-C問題解説
https://atcoder.jp/contests/abc256/tasks/abc256_c
総当たりと計算量を調べるのにとてもいい題材だなーと。
状況設定は次のような感じですね。
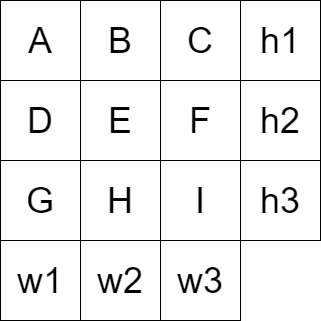
h1~w3までの行、列の合計値が与えられます(3~30)。A~Iに上手く数字を入れて、合計が等しくなるような組み合わせは何通りありますか?
さて、愚直にやるならAに1~30を入れて、Bに1~30を入れて……とIまで全部の総当たり、つまり(A,B,C,D,E,F,G,H,I)=(1,1,1,1,1,1,1,1,1)~(30,30,30,30,30,30,30,30,30)の30^9通り試せば答えが出る……んですが、ここで計算量と時間についてのお話をば。
一般に、コンピュータは1秒で10^7=1000万回程度(言語にもよると思います、C++は10^8回せるとかの噂)の処理が可能です。30^9=3^9*10^9ですから、総当たりおおよそ20000*10^9=2*10^13回の処理が行われて、ざっくり200万秒も時間がかかることになります。これはあまりにも効率の悪い方法と言わざるを得ません。
ではどうするのか?ということですが、そもそも総当たりの途中で、明らかに除外していいケースが存在します。例えばA~Cを決め打ちした段階でA+B+Cがh1にならなかった場合、その時点でD~Iを総当たりするのは時間の無駄です。ただこれだとまだ若干処理が重いんじゃないかなーと踏んでいます。検証はしていませんが……
方程式を解くにあたって、次の考え方は重要になってきます:
$A+B+C=h1 \Leftrightarrow C=h1-A-B$
これはどういうことかというと、A,B,h1の三つの値が分かっていて、なおかつh1はA+B+Cを満たす、ということが分かっていれば、Cの値は自然に一つに定まる、ということです。つまりCの値を1~30で総当たりする必要はないということですね。仮にこの時にCがマイナスの値になったら、それは既にA,Bの定め方がおかしいという判断で大丈夫なのです。なぜならA+Bがh1より大きくないとCはマイナスにならなくて、その状態からCを改めて正の数にしたところでh1になることはあり得ないからです。
さて、この考え方を用いて先ほどの図を少し書き換えてみます。
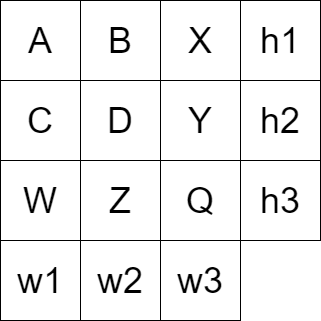
A,B,C,Dを定める。この時、$X=h1-A-B$
$Y=h2-C-D$
$W=w1-A-C$
$Z=w2-B-D$
が成立する。
なんと、A~Dの30^4通りを試すだけで8ヶ所が自動的に埋まることが分かりました。最後のQについても同様に考えてみると、$Q=w3-X-Y=h3-W-Z$となります。もしここで$w3-X-Y=h3-W-Z$ならQを埋めることで題意を満たしますし、そうでないならそもそもA~Dの組み合わせが悪かったということになります。これによって30^4通り=810000回の計算であり得る全ての組み合わせを検討することが出来ました。これは十分高速と言えますね。後は求められてる答えに沿うように題意を満たした組みあわせの数を覚えておく変数でも用意してあげればよいでしょう。
C問題以降では、このように愚直に計算すると実行時間が膨大になってしまいTLEになるというケースが発生します。上手くアルゴリズムを考えて高速に計算を行う、ということが競プロでは大事になりますね。逆に計算量の見積もりが出来れば、書く速度を重視して多少効率の悪いプログラムでも実行時間に間に合うだろう、という判断が可能になります(N=1000のN^3は間に合うか?N=300ならどうか?など)。
そんなところでした。大きなデータ扱うときには計算量抜きに語れないところがあるので、色々工夫してアルゴリズム考えられてるんだよーってお話でした。次はD問も面白かったので書きたいけど、いつになるかな……



ディスカッション
コメント一覧
まだ、コメントがありません