ABC255-B問題解説

2022年6月17日

問題はこちら。

https://atcoder.jp/contests/abc255/tasks/abc255_b

文章を読んでいると混乱する可能性があるので、まずは図をぶん投げます。

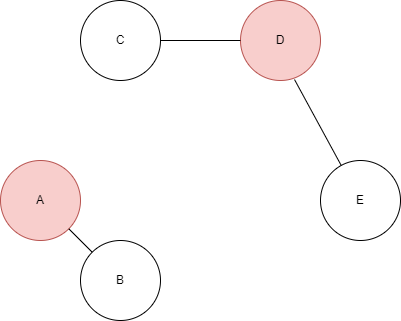
例えば $N=5, K=2,$
$A_1=1,A_2=4,$、5人の配置は図のA~Eのようになっているとします。また明かりを持たせた人を赤色にしています。

問題文は次のようになります。

「A~Eの五人が図のように立っている。ここで、AとDには明かりを持たせている。明かりの強さをいくつにすれば、全ての人が明かりの中に入るだろうか？」

さて、なんとなくD－E間の距離の強さのある明かりを持たせれば成功しそうなんですが（直感的な話なのでそう思わなくても問題ありません）、正直二次元上で話を考え始めるとBを始めたての人には難しいと思います。

というわけで問題をさらに簡単にして、一次元に落とし込み、さらに極端な例を三つ上げて考えてみます。簡単のために、それぞれの間の距離は1とします。

では、この三つの例の答えと等しくなるような条件は何でしょうか？例えば、「明かりを持っている人から一番離れている人」を照らせばいい、とすると最初の例は正解になりますが、二つ目、三つ目の例では正しくなさそうです。では「明かりを持っている人から一番近い人」を照らすと良いでしょうか？それも違いそうですね。う～ん、「明かりを持っている人」を基準にしてみると、どれも条件がバラバラですね。

では「明かりを持っていない人」を基準に考えてみましょう。彼らは少なくとも誰かに照らされてもらう必要がありますが、「一番近い明かりを持っている人」に照らされていればよい気がします。二つ目の例で距離を2、つまりCに照らしてもらうと考えた時、それよりも近いDにも照らされていることが分かります。当然誰か一人に照らしてもらえば条件を満たすので、より近い人に照らしてもらった方がお得ですね。

それではA~Eのそれぞれについて、その距離を調べてみましょう。なお、明かりを持っている人が誰かに照らしてもらうために必要な距離は、自分が明かりを持っているので0としています。そして[Aが照らしてもらうための距離、Bが照らしてもらうための～…,]という書き方をしています。

場合	距離	答え
一つ目の例	[0,1,2,3,4]	4
二つ目の例	[0,0,0,0,1]	1
三つ目の例	[0,1,2,1,0]	2

どうやら、全員の距離を取って、その中で一番大きいものを計算すれば良さそうです。後は二次元でも同じようになりそうなことが確認出来たら、実装して試してみましょう。本記事ではコードの実装に関しては省略します。

……と、まあこうやって複雑そうな条件が与えられたら、まずは具体的な例を挙げる、簡単な例や極端な例を考えてみる、その共通点を見つけてみる、といったことを行うことが大事だと思います。これはB問題に限らず、あらゆる場面で活躍する考え方だと思うので良ければ試してみてください。

おまけ：この考え方が数学的に正しい理由

書きたかったメインはこっちだったりしますが、競プロだと別に不要なので。記号の説明は後で行うので、とりあえず証明を書いちゃいます。アレルギーのある方は引き返すことをお勧めします。

(証明)$N\in\mathbb{N}, k\leq N$ とする. 適当に並べ替えることにより，明かりを持たせる人を $i=1,2,…,k$ としても一般性を失わない．$x,y\in\{1,2,…,N\}$ に対し，$d(x,y)$ を $x$ と $y$ の距離とする．この時，$$d=\max_{x\in\{1,2,…,N\}}\min_{i\in\{1,2,…,k\}}d(x,i)$$ がこの問題の解であることを示す．

示すこと：$$(1)\forall x\in\{1,2,…,N\},\exists i\in\{1,2,…,k\}, d(x,i)\leq d,$$ $$(2)\forall d’ < d, \exists (x,i)\in\{1,2,…,N\}\times\{1,2,…,k\}, d’ < d(x,i)$$

(1) 任意に $x$ をとる．各 $x$ について，次を満たす $i$ が存在する:$$d(x,i)=\min_{i\in\{1,2,…,k\}}d(x,i)$$

この $i$ に対し次が成立する: $$d(x,i)=\min_{i\in\{1,2,…,k\}}d(x,i)\leq\max_{x\in\{1,2,…,N\}}\min_{i\in\{1,2,…,k\}}d(x,i)=d$$ よって(1)が成り立つ.

(2) 最大値の定義より明らか．(1)とあわせて題意が示された．

証明が終わりました。では順番に見ていきましょう。

$N\in\mathbb{N}, k\leq N$ とする. 適当に並べ替えることにより，明かりを持たせる人を $i=1,2,…,k$ としても一般性を失わない……これは定義の段階ですね。問題では $A_i$ がばらばらに指定されていますが、最初の図を例にとると、BとDのラベルだけ入れ替えても状況設定は変わりませんよね。つまり明かりを持っている人を最初に並べて、残りの人を後から並べるという風に変えても良いということです（もちろんプログラムを書くときには与えられる順番が指定されているので工夫する必要がありますが）。これは単純に後の証明を楽にするための作業です。ちなみにちょっとカッコイイNは自然数をあらわす記号です。問題設定ではN=1000までですが、計算量の都合によるものなので証明自体はNが10万だろうと1億だろうと問題ありません。なお、$\in$ という記号は次のなかから一つ選ぶ、程度の認識で大丈夫です。

$x,y\in\{1,2,…,N\}$ に対し，$d(x,y)$ を $x$ と $y$ の距離とする……これも定義ですね。dという記号を使って二人の距離をあらわしている、と思えばいいです。例えば $d(A,B)=3$ ならAとBの距離は3です、ということを示しています。

この時，$$d=\max_{x\in\{1,2,…,N\}}\min_{i\in\{1,2,…,k\}}d(x,i)$$ がこの問題の解であることを示す……これが肝ですね。「「それぞれの人が誰かに照らしてもらうための一番短い距離」の中で一番遠い距離」のことを言っています。より細かく説明しましょう。右から順にみていきます。$d(x,i)$ は二人の距離ですね。そして $i$ は明かりを持っている人です。その中の $\min$、つまり最小値なので「明かりを持っている人との距離の最小値」を取っています。そしてそれらのすべての $x$ の $\max$、つまり距離が最大になるものを $d$ と置いているわけです。

示すこと：$$(1)\forall x\in\{1,2,…,N\},\exists i\in\{1,2,…,k\}, d(x,i)\leq d,$$ $$(2)\forall d’ < d, \exists (x,i)\in\{1,2,…,N\}\times\{1,2,…,k\}, d’ < d(x,i)$$……(1)は「すべての人が照らされている」こと、(2)「これより短い距離だと照らされない人が現れる」ことを示しています。$\times$ が挟まっていますが、$x$ は左から一つ、$i$ は右から一つ取っている、ということです。つまり「誰か一人と明かりを持っている人一人」の組を選んでいることになります。そしてこの二つの条件を合わせて示すことで $d$ が全員を照らすための最小値であることがいえるわけです。

(1) 任意に $x$ をとる．各 $x$ について，次を満たす $i$ が存在する:$$d(x,i)=\min_{i\in\{1,2,…,k\}}d(x,i)$$……証明の際は示すことに従って記号を用意していきます。ここで $\forall$ は「任意の」を意味しますから、照らされるべき人を一人選ぶことにしましょう。次に $\exists$ は「存在する」、つまりその次の条件を満たすような「明かりを持つ人」がいる、ということです。そしてその条件というのは、「それぞれの明かりを持っている人との距離の最小値」が等しくなる、ということです。当然距離が最小となる人を選べばこの式は満たされますね。

この $i$ に対し次が成立する: $$d(x,i)=\min_{i\in\{1,2,…,k\}}d(x,i)\leq\max_{x\in\{1,2,…,N\}}\min_{i\in\{1,2,…,k\}}d(x,i)=d$$ よって(1)が成り立つ…..ではその二人の距離 $d(x,i)$ についてわかることを考えてみましょう。今最初に一人 $x$ を選んで距離を考えましたが、全員選んで同じように距離を測って、その中の最大値を選ぶこと（つまり $d$ ）を考えてみると、最大値の方が等しいか大きくなりますよね（もし最大値の方が小さくなったら、それは最大値ではない！）。先ほどの式とあわせて左端と右端を見てみることで、(1)が示されていることが分かりました。

(2) 最大値の定義より明らか．(1)とあわせて題意が示された……最大値となるペア $(x,i)$ の距離が $d$ なわけですから、これより短い距離を指定したらこの二人のペアが照らされなくなってしまいますね。

以上がB問題を解くときに、そのコードでACが保証されることの説明でした。思ったより分量がすさまじいことになってしまいちょっと反省。いやしかし、丁寧に説明しようとするとどうしてもこうなるんですね……ちなみに証明が間違ってたら教えてください。嘘の証明書いてたら悲しくなるので……

今後も若干数学的なセンスがあった方が解きやすくなりそうだなー、みたいな問題があれば解説とおまけを書きたいですね。グラフ理論はぺーぺーですけど、数学やアルゴリズムの考え方が全くわからん！ってなる人の助けにでもなれば。